Anurag Shenoy
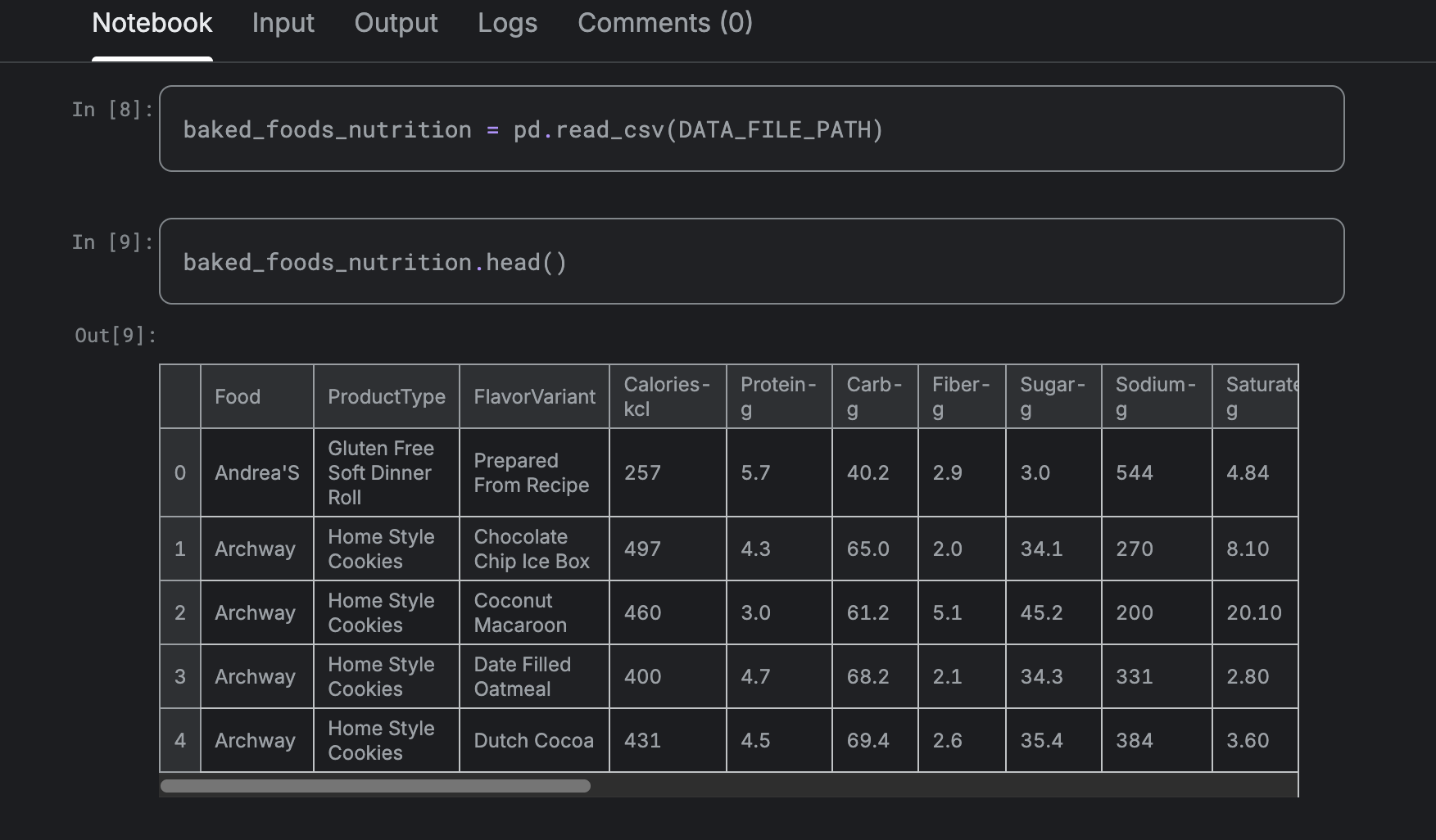
Data Science Crash Course — Dealing with Numerical Data

Data Science Crash Course — Dealing with Numerical Data

Overview

This post addresses the steps involved in Data Transformation.

It covers definitions of common terms, normalization, scaling, and binning and their pros and cons.

Feature Vector

An array of floating point values that the model ingests.

Usually feature-vectors use processed representations of the dataset's values.

Feature Engineering

The process of determining the best way to represent raw dataset values as trainable values is called feature engineering.

Normalization

Converting numerical values into a standard range.

Feature X may span values between 1 and 121 (like Age)

Feature Y may span values between 101 and 100000 (like monthly salary)

Why Normalize?

  • Models converge more quickly (Gradient descent may bounce if features have different ranges)
  • Infer better predictions
  • Avoid NaN trap — when feature value exceeds floating-point precision limit, the system sets the value to NaN.
  • Learn appropriate weights for each feature — Otherwise, the Model may pay too much attention to features with large ranges and larger values, compared to features with narrow ranges and smaller values.

Normalization Techniques

1. Linear scaling

Convert values from their natural range to a standard range such as 0 to 1 or -1 to +1.

x′=(x−xmin)/(xmax−xmin)x' = (x - x_{min}) / (x_{max} - x_{min})

Good for features like:

  • Features like Age.
  • Age has tight upper and lower bound.
  • Few outliers.

Bad for:

  • Features like Net Worth.
  • No good upper bound. Keeps changing.
  • Extremely wide range of values.
  • Several outliers.
  • Values aren't uniformly distributed across the range.

2. Z-Score scaling

A Z-score is the number of standard deviations from the mean. A value with a Z-score of +2.0 means that the value is 2 std above mean.

x′=(x−μ)/σx' = (x - \mu) / \sigma

σ = std ; μ = mean ; x' = z-score ; x = original value.

Good for:

  • Normally distributed feature like height.
  • Z-scoring is a decent choice for Net Worth. Not the best because most of the normally distributed values of Net Worth lie in a smaller range (maybe 10kto10k to 100k per year range), while other values are outliers. And the outliers can be huge. Clipping can help in this situation.

Bad for:

  • Features with Logarithmic distributions, exponential distributions or hyperbolic functions.

3. Log scaling

Computes logarithm of the raw value.

Usually ln or natural log is used i.e. Log to the base e. (e = 2.71828…)

Good for:

  • Features following Power-Law distribution or Zipf’s law.
  • Any feature that has ratings, or a frequency / ranking of some kind will usually be a goof candidate.
  • Examples: # of Movie ratings, Frequency of Word usage, City populations, Website traffic, Search engine usage etc.

Bad for:

  • Features following a normal distribution or a tightly bound linear range.

4. Clipping

Usually caps the value of outliers to a specific max value.

Good for:

  • Distributions which are mainly normal, but not completely normal.
  • Several extreme outliers, but most values are in a relatively narrow/moderate range.
  • Can be combined with Z-scoring.

Bad for:

  • When the outliers are fewer, and not mistakes.
  • Conversely, when the data is heavily tailed. Most values are on extreme ends.
  • The outliers are the values of interest — for example when detecting fraud or anomalies.
  • When domain knowledge suggests keeping outliers.

Binning

Converting numerical values into buckets of ranges.

Temperature ranges can often be binned to give a better understanding of which temperatures are considered too hot, too cold, or comfortable.

Example 1: A shopping mall can vary it’s Air conditioning temps and find out which temps lead to more sales.

Example 2: Ages can be binned into stages of life to better predict and infer financial or emotional outcomes.

Good for:

  • When we are more concerned with what a range of values represents as a meaning rather than what an individual value represents.
  • Example: Temperature of 36 degrees Celcius is “too hot” for humans, and may be the cause of lower productivity, and increased water consumption breaks. However we are less concerned with 36.2 degrees vs 37.1 degrees, and more concerned with a temperature of 32 and above, vs a temp range of 20 - 28, which is seen as a comfortable outdoor temperature.
  • Further, a range of 32 - 42 maybe a “too hot but manageable” range, but 42 and above may be “way too much”.

Bad for:

  • When there is no clear relationship between independent variable being considered for binning, and the dependent variable.

Steps for Numerical Data

  1. Visualize the data to find patterns and determine the distributions of various values.
  2. Statistically evaluate the data to evaluate potential features.
  3. Outliers: Find and decide whether to keep or remove.

References

  1. ML Crash Course by Google https://developers.google.com/machine-learning/crash-course